The elements that make up a parametric design involve nodes. This term, shared with computation and mathematics, has significant implications for the use of these programs and 

techniques. While we will not delve into all the terminology, as other authors have documented these elements more comprehensively, we still need a basic framework.

Woodbury (2011) defines nodes as schemata, or objects containing properties. In parametric design, a node is the minimal unit of information. An algorithm is an operation, evaluation, or sequence that instructs a program on how to process data or perform tasks.

A parametrically designed solution can be represented as a node graph, where each node corresponds to a specific property or value. These values propagate in a cascading manner, with each successive node being influenced by the properties of the preceding nodes and, in turn, affecting all subsequent nodes.

Nodes can also represent the intersections of systems. In this context, nodes describe the relationships and dependencies among various elements, containing more complex information that is dependent on other nodes.

This process can be expressed as it follows:

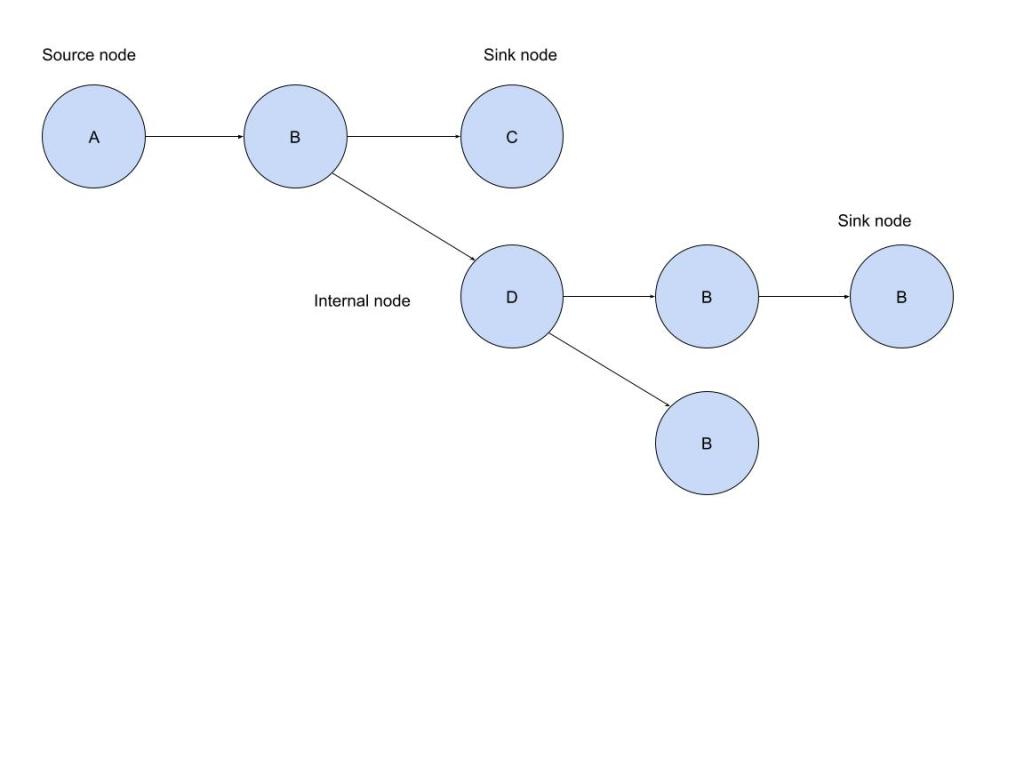
The figure above represents a basic node graph where A is a source node preceding B. B is an expression or internal node resulting in C, which is a sink node without successors. Any changes in A or B propagate to C and D. Other nodes are also identified, but they can still be defined in the same manner.

In this particular case, we have a directed graph in which the elements do not refer back to previous elements, thus avoiding circular logic.

All the possible combinations that can be obtained from a parametric design configured in this way are contained and generated by the algorithms defined in these graphs. This key idea builds the fundamental concept of parametric design logic and explains how the different programs interact.