Formally, we can describe the world in three dimensions by constructing sequential definitions that begin with a point and a vector. The mathematical concepts underlying this understanding are well-established and occupy a significant portion of the early years of education in many architecture and engineering programs.

However, I would prefer not to approach this topic from a hard-sciences perspective for two reasons:

1. Accurately describing the conception of space from a mathematical perspective involves a substantial amount of theory and explanations, which have already been thoroughly covered by many experts with far greater authority than myself.
2. As an architect, I find the concept of pictorial generation, developed by Paul Klee, much easier to understand. It also serves as a very good summary of mathematical principles.

On “The thinking eye”, Klee expresses: I begin where all pictorial form begins: with the point that sets itself in motion.

Building on this elegant thought, we can articulate the following:

This point, endowed with agency, creates a line through its movement, thus bringing forth the first dimension (1D).

This restless line then shifts, giving rise to planes (2D).

The gathering of these animated planes creates a volume (3D).

The interplay and interaction of these elements in our world constitute the entirety of the pictorial understanding of nature that we can access. This understanding forms the basis of our representations and, of course, affects how we use our tools and 3D programs.

The image below, captured at the Bjørvika library in Norway, vividly exemplifies this concept. The room itself can be seen as a volume, while each surface can be perceived as a plane, depending on the scale of observation.

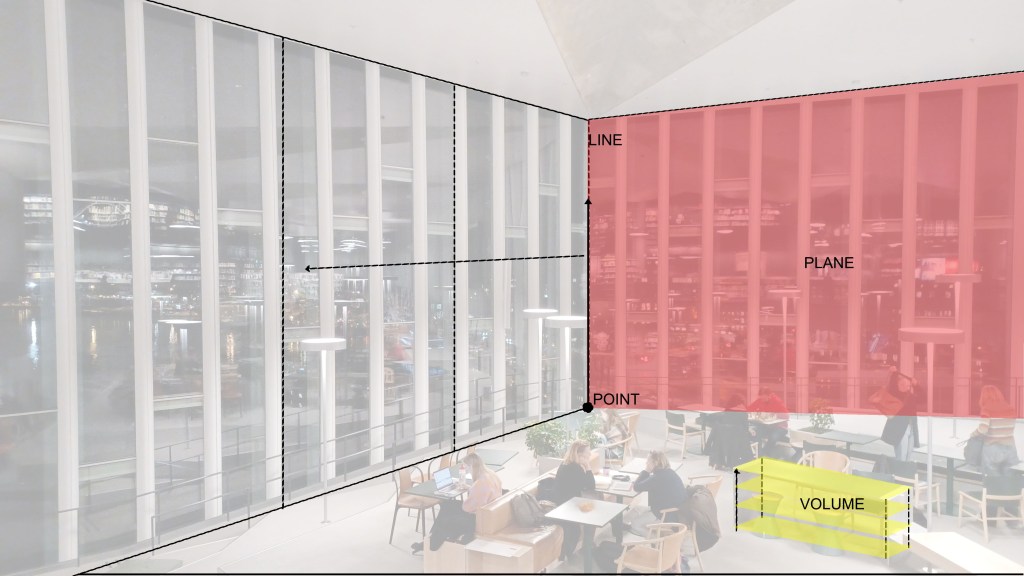
I firmly believe that a fundamental understanding of these interactions greatly facilitates our comprehension and use of drawing programs and 3D space.